فیزیک بدون ترس

اگر در تلاش هستید تا ذهنی خود را برای یک پرش بانجی آماده کنید ، این راهنما را برای مبتدیان با ترس و اضطراب بخوانید.

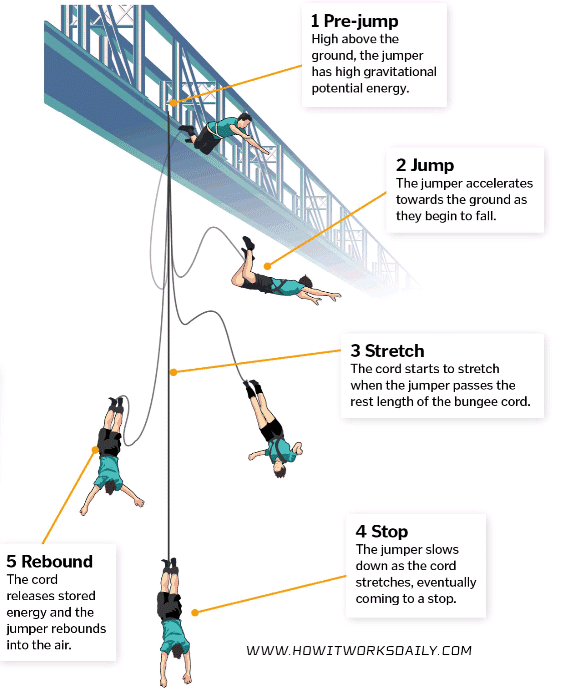
پرش بانجی چگونه عمل می کند
چهار مؤلفه اصلی وجود دارد که شما باید نگران آنها باشید. وزن ، طناب ، مهار ، و سپس خود پرش. در اینجا نحوه ترکیب همه آنها به شما امکان می دهد با خیال راحت پرش کنید.

1. وزن شما
شما توسط اپراتور بانجی وزن می شوید ، گاهی اوقات حتی دو بار. دلیل انجام این کار این است که به آنها اجازه دهید طول طناب مرد نیاز را محاسبه کنند .

2. طناب
تارهای بانجی از لاستیک و پارچه های مخصوص نظام ساخته شده اند. 

طناب با استفاده از تجهیزات تخصصی بسیار شبیه به آنچه در دنیای کوهنوردی استفاده می شود ،  به سکوی پرش وصل خواهد شد.

3. مهار
طناب با استفاده از مهاربندها به شما وصل خواهد شد. بیشتر اپراتورهای تجاری از دو بند استفاده می کنند. یکی به مچ پا متصل است و دیگری به بدن.

4- پرش
سپس اپراتورها تسمه های شما را به طناب وصل می کند.و پرش صورت میگیرد

شتاب آزاد سقوط بزرگتر از g

شکل زیر برای این تجزیه و تحلیل نمایش ساده ای طناب بانجی ، در موقعیت اولیه (1) ، قبل از پرش  را نشان می دهد. پرش کننده به عنوان یک جسم با جرم M. نشان داده شده است.طناب به دو قسمت به طول L / 2 تبدیل شده، که با خم در قسمت پایین شعاع نشان داده شده است. سمت چپ طناب bungee به یک تکیه گاه ثابت متصل است. جرم طناب بانجی  m است. شتاب ناشی از گرانش g است (برابر با 9.8 ). قرارداد علامت "بالا" به عنوان مثبت و "پایین" به عنوان منفی است.

فرضیات اضافی در این تحلیل عبارتند از:

• پرش کننده M در طول پایین آمدن به طور عمودی به سمت پایین سقوط می کند ، و قسمت طناب در حال سقوط  به طور مستقیم در زیر قسمت اولیه  باقی می ماند.

• اصطکاک و مقاومت هوا را می توان نادیده گرفت.

• شعاع R خم نسبت به طول قسمتهای مستقیم طناب بانجی كوچك است. بنابراین ، طول طناب bungee تقریباً L است.

• در طول قسمت اولیه طناب ، کشش اضافی که در قسمت حلق آویز طناب وجود دارد زیرا بیشتر از وزن خود را پشتیبانی می کند ، ناچیز است. این بدان معنی است که تغییر در انرژی پتانسیل الاستیک قسمت معلق طناب  به اندازه کافی کوچک است که در حفظ معادله انرژی نادیده گرفته می شود. این معادله (1) در تحلیل ارائه شده در زیر است.

شکل زیر برای این تجزیه و تحلیل نمایانگر طناب بانجی پس از پرش او است. این به عنوان موقعیت (2) مشخص شده است. موقعیت پرش کننده وطناب به عنوان تابعی از y تنظیم می شود که موقعیت جهنده M نسبت به نقطه پرش است (به عنوان موقعیت عمودی اصلی وی انتخاب شده است). طول مقاطع مستقیم طناب به عنوان تابعی از y داده می شود و براساس هندسه مسئله است. سرعت عمودی جامپر به صورت v و شتاب عمودی به عنوان a داده می شود. با توجه به هندسه ، سرعت عمودی نوک پایینی خم v / 2 است و شتاب عمودی نوک پایینی خم a / 2 است.

از آنجا که اصطکاک و مقاومت هوا صرفنظر می شود ، فیزیک موجود بین موقعیت ها (1) و (2) که می تواند با استفاده از پایستگی  انرژی برای سیستم ، که متشکل از طناب و پرش کننده  است ، تجزیه و تحلیل کرد. این به ما امکان می دهد تا سرعت v پرش را به عنوان تابعی از y تعیین کنیم. از آنجا که اصطکاک و مقاومت هوا صرفنظر شده است ، تنها نیرویی که روی سیستم کار می کند ، گرانش است.

معادله برای پایستگی انرژی به شرح زیر است:

 که:

T1 انرژی جنبشی سیستم است ، در موقعیت (1)

V1 انرژی پتانسیل گرانشی سیستم است ، در موقعیت (1)

T2 انرژی جنبشی سیستم است ، در موقعیت (2)

V2 انرژی پتانسیل گرانشی سیستم در موقعیت (2) است

از آنجا که سیستم ازحال سکون رها میشود (1) انرژی جنبشی است

انرژی پتانسیل گرانشی سیستم در موقعیت (1) شامل پتانسیل گرانشی طناب بانجی بعلاوه

پتانسیل گرانشی پرش کنندهMکه صفر است زیرا او در همان ارتفاع داده قرار دارد.

بدین ترتیب،

توجه داشته باشید که این مقدار منفی است زیرا مرکز جرم طناب بانجی زیر مبدا است.

برای راحتی چگالی طناب را به عنوان ρ تعیین کنید که به عنوان جرم در طول واحد تعریف می شود. این توسط داده شده است

انرژی جنبشی سیستم در موقعیت (2) برابر

اولین اصطلاح در سمت راست ، انرژی جنبشی بخش مستقیم طناب در زیرجرم (M) است. این بخش از طناب در سرعت حرکت می کند. اصطلاح دوم در سمت راست ، انرژی جنبشی جامپر M است ، که او نیز با سرعت v حرکت می کند.

انرژی پتانسیل گرانشی سیستم در موقعیت (2) توسط داده می شود

یک بار دیگر به خاطر داشته باشید که ما از توده نسبتاً کمی طنابد در انتهای خم چشم پوشی می کنیم. بنابراین این توده در عبارات مربوط به انرژی جنبشی و پتانسیل داده شده در بالا نشان نمی دهد.

معادلات (2) - (5) را در معادله (1) جایگزین کرده و برای V حل می کنیم

این عبارت به راحتی سرعت v پرش کننده را به موقعیت عمودی y خود مرتبط می کند. یک بار دیگر به خاطر داشته باشید که y <0 مطابق با  علامت استفاده شده.

قدم بعدی در این تجزیه و تحلیل ، اعمال اصل ضربه و حرکت برای محاسبه شتاب جامپر بانجی (a) است.

برای راه‌اندازی این تجزیه و تحلیل ، بخشی از سیستم را با استفاده از یک نوع کنترل حجم تحلیل ، جدا می کنیم که بخشی از سیستم (متشکل از جرم M و طناب) را که می خواهیم آنالیز کنیم ، جدا می کند. این حجم کنترل ثابت با هوشمندی انتخاب شده است تا بتوانید راحت تر شتاب a بانجی را تعیین کنیم ، زیرا او سقوط می کند.

در این حجم کنترل انتخاب شده ، طنا می تواند به صورت "در حال جریان" از مرز سیستم (که توسط خط متراکم نشان داده می شود) در پایین ترین قسمت خم ، جایی که کشش طناب  افقی است تصور شود. اجزای عمودی نیرو در این مکان بسیار کوچک فرض می شود که فرض خوبی برای طناب ها و سازه های شبیه طناب است.

از آنجا که فقط نیروهای عمودی که روی این سیستم کار می کنند (محصور شده توسط حجم کنترل) a را تحت تأثیر قرار می دهند ، نیازی به تنش T نیست. این باعث صرفه جویی در زمان محاسبه می شود.

نیروی عمودی که روی سیستم محصور شده در حجم کنترل اعمال می شود ، گرانش است که به راحتی می توان آن را حساب کرد.

مرحله بعدی در این تجزیه و تحلیل استفاده از حساب برای تنظیم معادلات حاکم است.

شکل زیر را در نظر بگیرید. دو مرحله (1) و (2) "حالت" سیستم را در زمان t و زمان t + dt نشان می دهد ، جایی که dt یک مرحله زمانی بسیار کوچک (نامتناهی) است.

بار دیگر ، ما از جرم بخش طناب شعاع R در انتهای خم چشم پوشی می کنیم.

بین (1) و (2) ، تغییر در حرکت خطی در جهت y همه ذرات موجود در سیستم (تعریف شده توسط حجم کنترل) ، به دلیل جمع نیروهای خارجی در جهت y است که بر روی تمام ذرات موجود در سیستم.

ما می توانیم با استفاده از حساب و اصل تکانه و حرکت آن را به صورت ریاضی بیان کنیم:

 که:

mcv جرم ذرات داخل حجم کنترل است ، در مرحله (1)

ΣFy مجموع نیروهای خارجی در جهت y است که بر روی تمام ذرات موجود در حجم کنترل عمل می کند

dmcv تغییر جرم ذرات درون حجم کنترل ، بین (1) و (2) است. توجه داشته باشید که dmcv <0 از جرم ذرات درون حجم کنترل در حال کاهش است.

dmp جرم ذراتی است که به سمت خارج از حجم کنترل "جریان یافته" است

dv تغییر در سرعت عمودی ذرات درون حجم کنترل ، بین (1) و (2) است. توجه داشته باشید که (نادیده گرفتن خم) تمام ذرات درون حجم کنترل با همان سرعت عمودی حرکت می کنند

عبارت فوق را گسترش دهید. در حد dt → 0 ممکن است از دو اصطلاح "مرتبه دوم" dmcvdv و dmpdv / 2 صرفنظر کنیم. تقسیم بر dt و ساده کنید. ما گرفتیم

حال ، جرم ذراتی که از حجم کنترل خارج می شوند باید یک مقدار مثبت باشند. از این رو،

این بدان معنی است که

جایگزین معادله بالا را در معادله (7) و ما

اکنون،

این را در معادله قبلی جایگزین کنید و دریافت کنیم

اکنون،

مجموع نیروهای خارجی در جهت y که بر روی ذرات حجم کنترل عمل می کنند ، نیروی گرانشی است. این توسط داده شده است

معادلات جایگزین (9) - (11) را به معادله (8) تبدیل می کنیم و می گیریم

حل برای. این به ما می دهد

همانطور که می بینید شتاب a از g بیشتر است.

توجه داشته باشید که این معادله فقط بین y = 0 و y = -L معتبر است.

برای به دست آوردن عبارتی در رابطه با تعویض y (6) به معادله (13). این به ما می دهد

بار دیگر ، y <0 همانطور که در قرارداد علامت تعریف شده است.

برای راحتی بیشتر μ = m / M معادله فوق سپس تبدیل می شود

موقعیت y = -L نقطه ای است که شتاب a حداکثر باشد. به عنوان مثال ، اگر طناب هم وزن پرش کننده بانجی باشد ، حداکثر شتاب تقریبی 1.6g است.

اگر a = d2y / dt2 را در معادله فوق جایگزین کنیم ، معادله دیفرانسیل معمولی را بدست می آوریم که می توانیم عددی را برای تعیین y به عنوان تابعی از زمان حل کنیم. راه حل در شرایط t = 0. تحت شرایط اولیه قرار دارد. این شرایط اولیه عبارتند از: y = 0 و dy / dt = v = 0 (سیستم از حالت استراحت شروع به سقوط می کند).

حتی اگر این تجزیه و تحلیل ساده شده باشد ، نتیجه ای که a> g معنا می یابد ، زیرا تغییر سرعت (از v به v / 2) طناب در هنگام حرکت به دور خم به معنای این است که باید در طناب تنشی وجود داشته باشد که "بکشد. " بطرف بالا. این تنش باعث کاهش سیم در محل خم می شود. این کشش به نوبه خود باعث می شود بخش طناب بالای خم و جسم سرعت بیشتری به سمت پایین از g به سمت پایین بتابد.